Characteristics of AC

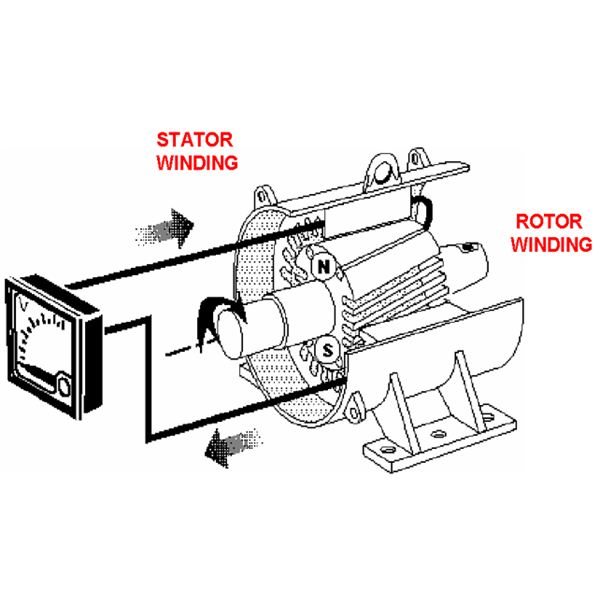
Alternating voltage may be generated by rotating a coil in a magnetic field or by rotating a magnetic field within a stationary coil. The value of the voltage generated depends, in-each case, upon the number of turns in the coil, strength of the field and the speed at which the coil or magnetic field rotates.

Equations of the Alternating Voltages and Currents:

Consider a rectangular coil having N turns and rotating in a uniform magnetic field with an angular velocity of ω radian / second as shown in Figure. Maximum flux Φ_m is linked with the coil when its place coincides with the X-axis.

In time t seconds, this coil rotates through an angle θ = ωt.

In this deflected position, the component of the flux which is perpendicular to the plane of the coil is Φ = Φ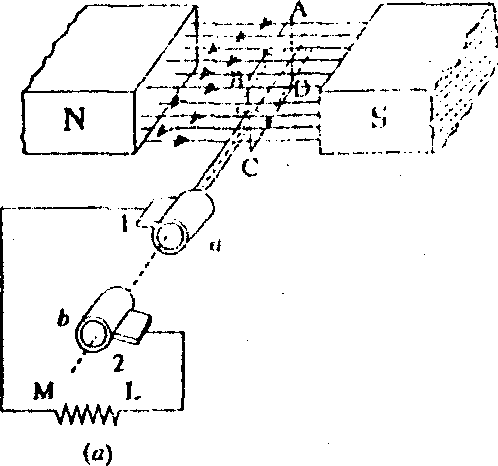_m cos ωt.

Hence, flux linkages of the coil at any time are NΦ = NΦ_m cos ωt.

According to Faraday's Laws of Electromagnetic Induction, the e.m.f induced in the coil is given by the rate of change of flux-linkage of the coil. Hence, the value of the induced e.m.f at this instant (i.e where θ = ωt) or the instantaneous value of the induced e.m.f is

e =    ωNΦ_m sin ωt   volt                 ----------(i)

When the coil has turned through 90° i.e. when θ = 90°, then sin θ = 1, hence ‘e’ has maximum value, say E_m. Therefore, from above equation we get

E_m = ωNΦ_m = 2лfNB_mA volt

f= frequency of rotation of the coil in rev/second. Substituting this value of E in Eq (i) we get

e = E_m sin ωt

Similarly, the equation of the induced alternating current is

i = I_m sin ωt

provided the coil circuit has been closed through a resistive load.